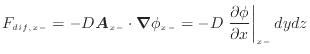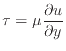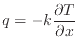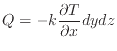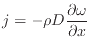


Next: 2.1.7 微小項の取り扱い
Up: 2.1 保存量
Previous: 2.1.5 出入の項 対流
対象とする物理量の値に分布がある場合に、流体の流れではなく分子運動によって物理量が運ばれるのが拡散である。拡散は流れによる輸送ではないので、拡散のみの場合は流れは起きない(流体の速度はゼロ)。物質拡散では、分子が入れ替わることにより物質が運ばれる。
水槽の上部と下部で水とインクの層を乱さないように静かに作ったとき、流れを起こさなくても、次第に水とインクの境界が曖昧になり、長い時間の後には、水とインクが混ざり、水槽の中身はすべて薄いインクとなる。流れがないときにゆっくりと混ざる現象を拡散と呼ぶ。水の入った水槽に、ゆっくりとインクを一滴落とした後に、インクが薄くなり、広がっていくのも拡散である。
拡散の影響は式(2.8)の“拡散による出入”で表され、運動量の拡散(粘性2.2)、エネルギーの拡散(熱伝導)、物質拡散がある。それぞれの物理量に勾配があるとき、拡散による輸送量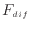 は拡散係数
は拡散係数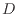 [m
[m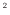 /s](運動量では動粘性係数、エネルギーでは熱拡散係数、物質では物質拡散係数)により、次式により表される2.3。
/s](運動量では動粘性係数、エネルギーでは熱拡散係数、物質では物質拡散係数)により、次式により表される2.3。
ここで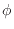 は単位質量あたりの対象とする物理量を表す。図2.1の左側の面を考えると、
は単位質量あたりの対象とする物理量を表す。図2.1の左側の面を考えると、
この拡散の項は運動量、エネルギー、化学種の保存式でそれぞれ以下のようになる。
- 運動量 (ニュートンの粘性法則)
粘性によるx方向速度成分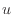 [m/s]のy方向の速度勾配による剪断応力
[m/s]のy方向の速度勾配による剪断応力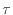 [N/m
[N/m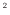 ]は粘性係数
]は粘性係数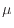 [Pa
[Pa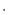 s]により次式で表される。
s]により次式で表される。
- エネルギー (フーリエの法則)
x方向の温度勾配による熱流速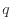 [W/m
[W/m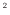 ]は熱伝導率
]は熱伝導率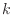 [W/(K
[W/(K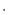 m)]により
m)]により
伝熱量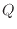 [W]は伝熱の面積
[W]は伝熱の面積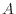 [m
[m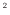 ]とともに次式で表される。
]とともに次式で表される。
- 化学種 (フィックの拡散法則)
質量流束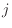 [kg/(m
[kg/(m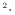 s)]は濃度(質量分率)
s)]は濃度(質量分率)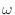 [-]([kg/kg])のx方向の勾配により拡散係数
[-]([kg/kg])のx方向の勾配により拡散係数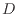 [m
[m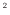 /s]を用いて次式で表される。
/s]を用いて次式で表される。



Next: 2.1.7 微小項の取り扱い
Up: 2.1 保存量
Previous: 2.1.5 出入の項 対流
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
![]() は拡散係数
は拡散係数![]() [m
[m![]() /s](運動量では動粘性係数、エネルギーでは熱拡散係数、物質では物質拡散係数)により、次式により表される2.3。
/s](運動量では動粘性係数、エネルギーでは熱拡散係数、物質では物質拡散係数)により、次式により表される2.3。