2 積立投資

積立投資として、定期的に定額を積み立てる場合の計算は少し難しい。まず、積立投資において資産額が入金額の二倍になる年数を計算していこう。 一年に一回入金して、年の利回りを$y$ %として考える。1年目の資産額を計算しよう。年初に入金するとして利回りのかかった年末の額を計算する。

2年目の資産額は1年目の資産額に一回の入金額が加わり、さらに$y$ %の利回りがかかるので次のように表される。

$T$年目の資産額は、毎年、一回の入金額が加わり$y$ %の利回りがかかるので次のように表される。等比数列となるので等比数列の和の公式を用いて変形する。

$T$年目の入金額は次式で表される。

資産額が入金額の2倍になる年数を知りたいので、次式を変形していく。

上式のように$T$と$y$の関係が求められたが、上式の形から左辺にのみ$T$がある$T=\mathrm{\cdots }$の形に変形することはできない。グラフを書くために、パソコンを使いニュートン法でyを0.01刻みで計算した。

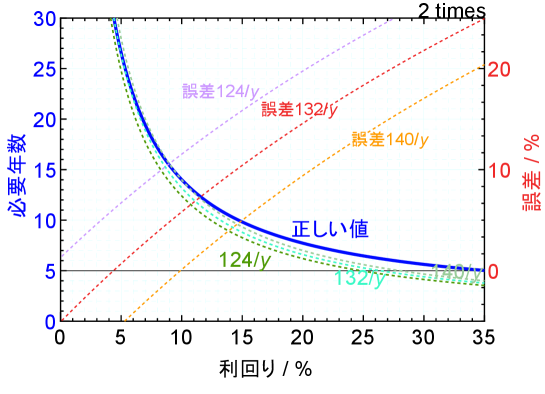
図4に積立投資で入金額になるまでの利回りと年数の関係と、72の法則と同じ形で、124/$y$、132/$y$、140/$y$を利回り$y$で割った値で求めた線を一緒に描いている。 図のように一括投資のようにきれいな近似は見られない。72の法則の図1では、利回りが0 % - 20 %の範囲では誤差が±5 %程度以内に収まっているが、132/yの近似では金利20 %で誤差が15 %近く、必要な年数では一年以上のずれがある。

そこで式の形を変えて(定数／利回り＋定数)の形で考えると、かなりよい予測ができる。次式で表される関係と比較してみよう。

図5に上式による近似との比較を示している。赤い線が正しい値、青い点線が上式による近似の値、また定数を120、124、125、126、130にした場合の誤差を右軸で表している。式(5)による近似はグラフ中の全ての範囲で±1 少し形は複雑になってしまうが、積立投資の場合は125を利回りで割って一年半をたす「125たす1.5の法則」で良い近似ができる。