1 一括投資

二倍になるまでの年数と利回りの関係の72の法則で知られている近似の関係が、どの程度正しいのか見てみよう。近似の式は、年の利回りを$y$ %、二倍になるまでの年数を$T$とすると、次式で表される。

一括でまとめて投資した資産が二倍になるまでの年数はどのように求められるだろうか。まず、$T$年後の資産額から計算する。始めの資産額が年に$y$ %増えるので1年目は次のように求められる。

上式で$y$は%であるので100で割り1に足している。例えば10 %増えるのであれば 1 + 0.1 = 1.1 と一年で1.1倍になる。

2年目には1年目の資産にさらに$y$ %の利回りがかかるので次のように計算される。1年目の資産額には先に求めた式(2)を代入する。

毎年利回りがかかるので、T年目の資産額は次のようになる。

始めの資産額に比べて$T$年後に二倍になっているので次の関係になる。ここに式(3)を入れて変形していく。

上式のように二倍になるまでの年数$T$と利回り$y$の関係が求められた。しかし、logの底に変数が入っていると関数電卓や表計算ソフトでも計算ができないので、logの底が10になるように変形する。logの底を変える方法については後Aに詳細な説明をしている。

上式(4)の形であれば表計算ソフトなどでも計算ができる。この正しい値を示している式と比べることで、72を利回りで割った式(1)がどの程度正確であるか、グラフを使って確認しよう。

正しい関係を表している式(4)と、近似を表している72の法則の式(1)を、必要年数と利回りのグラフに描いた(図1)。

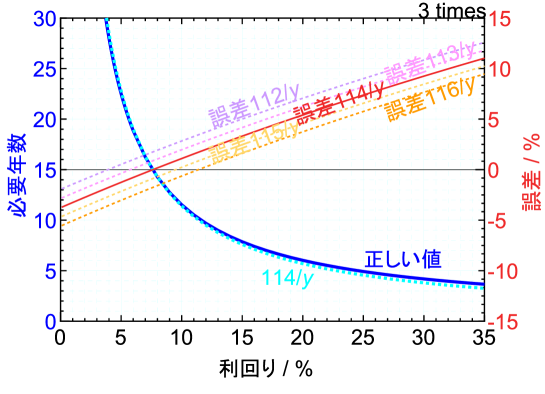
図中の青い実線が正しい値を示している式(4)の値で、水色の点線が近似を表している72の法則の式(1)の値である。青い実線と水色の点線はほぼ重なっていて、72の法則はよい近似であることがわかる。より詳しく差を表すため、右軸に誤差((正しい値 - 近似値) / 正しい値×100)をとり赤色の実線で誤差を同じグラフ中に示している。誤差は利回り8 %付近で0 %であり、ほぼ正確な値をしめしている。利回り19 %では誤差は5 %程度で必要年数が4年程度であるから、4年の5 %で0.2年、2.4ヶ月程度と、二倍になる期間を概算するには十分な小ささだろう。

割る数字が72からずれたら誤差はどうなるだろうか。同じ図1に70から74を割った場合の正しい値との誤差をそれぞれ異なる色の点線で示している。72では利回り8 %付近で一番正確であったが、71では5 %付近、73では11 %付近で一番正確な値となる。72ではなく、73や74を割った年数でも実用上問題はなさそうではあるが、利回りで割る際には72が約数が多いため計算しやすいという点では一番使いやすいのかもしれない。

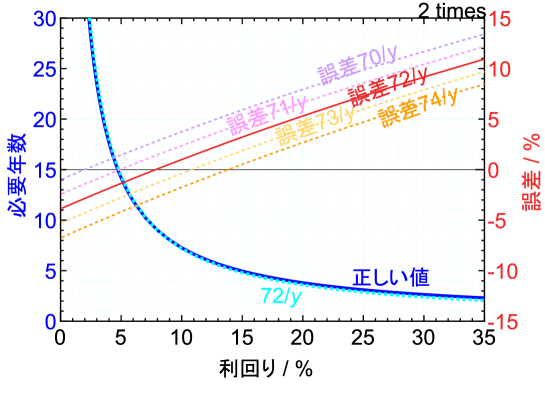
三倍になるまでの年数と利回りの関係はどのように表されるだろうか。図2に先ほどと同じように正しい値と近似として114を利回りで割った値のグラフを示している。正しい値を示している青い実線と、114を利回りで割った近似の水色の点線は良い一致を示しているように見える。図1と同じように利回りが8 %程度で誤差が0 %程度になっており、全体での誤差の程度も近い。三倍になるまでの年数は114を利回りで割ればある程度の精度で求められると言えるだろう。

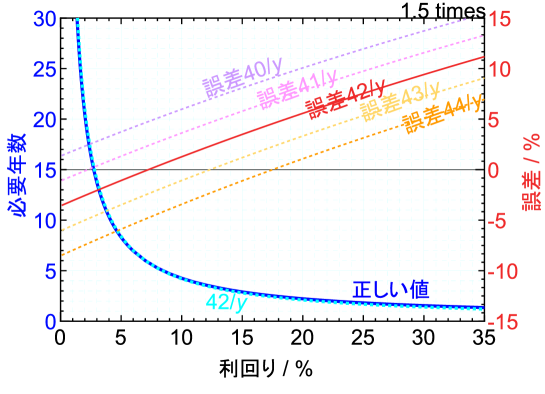
1.5倍になるまでの年数と利回り、誤差との関係を図3に示す。1.5倍になるまでの年数は42を利回りで割ることである程度の精度で求められることが分かる。