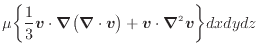


Next: 参考文献
Up: A. 付録
Previous: A.2 エネルギー保存式での計算の詳細
A.3 散逸エネルギー
2.4.4節のように、コントロールボリュームでの時間あたりの仕事は面に作用する力と流速の内積で表される。
一項目
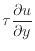 は、応力と速度の変化量である。速度の変化量は垂直方向の変化なので、変形を表している。流体を変形させる仕事であるため、内部エネルギーに変換される。二項目
は、応力と速度の変化量である。速度の変化量は垂直方向の変化なので、変形を表している。流体を変形させる仕事であるため、内部エネルギーに変換される。二項目
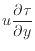 は、応力の変化量と速度である。応力の変化で方向は変わらないため、流体を加速させる仕事となる。このように一項目は流体を変形させ粘性により熱となり内部エネルギーに変換される。これを散逸と呼ぶ。二項目は加速させる仕事で、運動エネルギーになる。
は、応力の変化量と速度である。応力の変化で方向は変わらないため、流体を加速させる仕事となる。このように一項目は流体を変形させ粘性により熱となり内部エネルギーに変換される。これを散逸と呼ぶ。二項目は加速させる仕事で、運動エネルギーになる。
散逸項と加速項の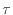 に、それぞれ次式を代入する。
に、それぞれ次式を代入する。
散逸項のみを表すと次式となる。
上式のように面に垂直な応力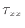 、
、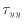 、
、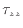 の入った項は流体の伸縮となる。流体が伸縮することで変形し内部エネルギーへと変換される。面に平行な応力
の入った項は流体の伸縮となる。流体が伸縮することで変形し内部エネルギーへと変換される。面に平行な応力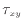 、
、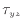 、
、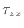 の入った項は流体の剪断変形となる。流体が剪断変形することで内部エネルギーへと変形される。流体の収縮や剪断変形については杉山らの教科書[2]に分かりやすくまとめられている。
の入った項は流体の剪断変形となる。流体が剪断変形することで内部エネルギーへと変形される。流体の収縮や剪断変形については杉山らの教科書[2]に分かりやすくまとめられている。
加速項のみを表すと次式となる。
散逸についての詳細は日野の教科書[3]を参照すること。



Next: 参考文献
Up: A. 付録
Previous: A.2 エネルギー保存式での計算の詳細
この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。
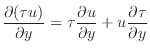
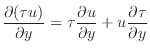
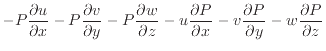
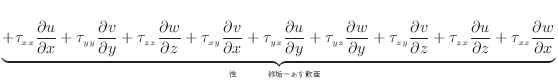
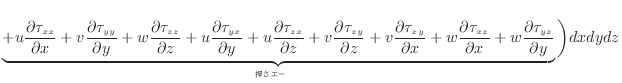
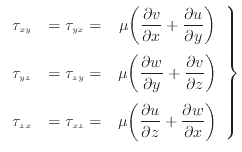
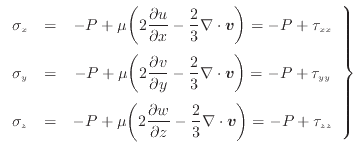
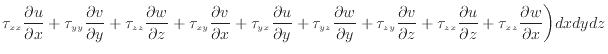
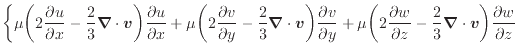
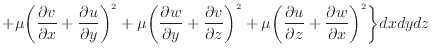
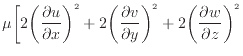
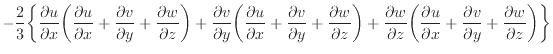
![$\displaystyle + \bigg( \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\par...
...\partial u}{\partial z} + \dfrac{\partial w}{\partial x} \bigg)^2 \bigg] dxdydz$](img801.png)
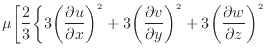
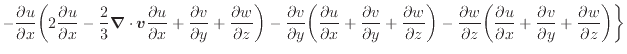
![$\displaystyle + \bigg( \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\par...
...\partial u}{\partial z} + \dfrac{\partial w}{\partial x} \bigg)^2 \bigg] dxdydz$](img801.png)
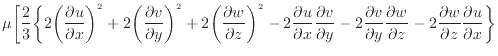
![$\displaystyle + \bigg( \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\par...
...\partial u}{\partial z} + \dfrac{\partial w}{\partial x} \bigg)^2 \bigg] dxdydz$](img801.png)
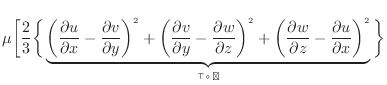
![$\displaystyle \underbrace{ + \bigg( \dfrac{\partial v}{\partial x} + \dfrac{\pa...
...c{\partial w}{\partial x} \bigg)^2 }_{流体の剪断変形(ずり変形)} \bigg] dxdydz$](img806.png)
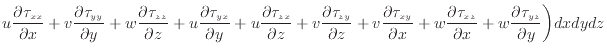
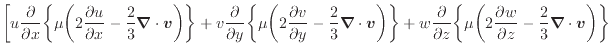
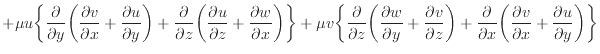
![$\displaystyle + \mu w \bigg\{ \frac{\partial }{\partial x} \bigg( \frac{\partia...
...rtial y} + \frac{\partial v}{\partial z} \bigg) \bigg\} \bigg] dxdydz \nonumber$](img816.png)
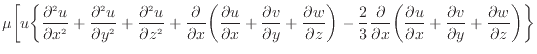
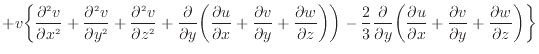
![$\displaystyle + w \bigg\{ \frac{\partial ^2 w}{\partial x^2 } + \frac{\partial ...
...rtial y} + \frac{\partial w}{\partial z} \bigg) \bigg\} \bigg] dxdydz \nonumber$](img819.png)
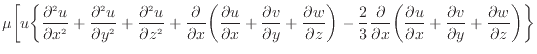
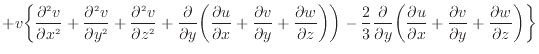
![$\displaystyle + w \bigg\{ \frac{\partial ^2 w}{\partial x^2 } + \frac{\partial ...
...rtial y} + \frac{\partial w}{\partial z} \bigg) \bigg\} \bigg] dxdydz \nonumber$](img819.png)
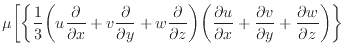
![$\displaystyle + \bigg\{ u \bigg( \frac{\partial ^2 u}{\partial x^2 } + \frac{\p...
... } + \frac{\partial ^2 w}{\partial z^2 } \bigg) \bigg\} \bigg] dxdydz \nonumber$](img821.png)