• 学問 -top-

2.3.3 表面に作用する力

それぞれの面に作用する力を、図2.5に示すように面に垂直方向応力を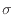$\sigma$ [Pa]、平行な剪断応力を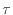$\tau$ [Pa]とし、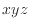$xyz$ 方向の成分に分けて考える。外に向かう力が正となるように方向を決める。

図 2.5: Control Volume

下記の式(2.58)^2.5と式(2.59)の関係[1]を用いる。

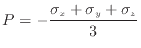$$P = - \frac{ \sigma_x + \sigma_y + \sigma_z} {3}$$ (2.57)

垂直応力と剪断応力の釣り合いより次式となる。

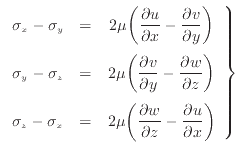$$\left. \begin{array}{ccc} \sigma_x -\sigma_y & = & 2 \mu \bigg( \... ...tial w}{\partial z} - \dfrac{\partial u}{\partial x}\bigg) \end{array} \right\}$$ (2.58)

式(2.58)へ式(2.59)を変形して代入し、それぞれの方向の垂直応力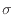$\sigma$ [Pa]は次のように表される。

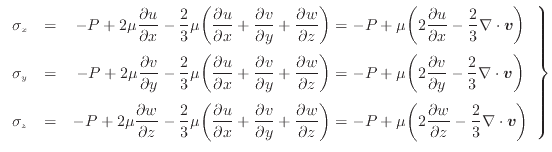$$\left. \begin{array}{ccc} \sigma_x & = & - P + 2 \mu \dfrac{\part... ...al w}{\partial z}- \dfrac{2}{3} \nabla \cdot \bm{v} \bigg) \end{array} \right\}$$ (2.59)

平行方向の剪断応力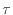$\tau$ [Pa]はニュートンの粘性法則より、それぞれ次のように表される[1]。図2.5のように下添え字の最初の文字が面に垂直な軸を、次の文字が方向を表している。

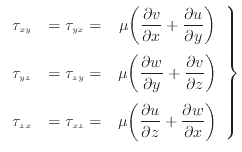$$\left. \begin{array}{ccc} \tau_{xy} & = \tau_{yx} = & \mu \bigg( ... ...ial u}{\partial z} + \dfrac{\partial w}{\partial x} \bigg) \end{array} \right\}$$ (2.60)

• 学問 -top-

この図を含む文章の著作権は著者にあり、クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 3.0 非移植 ライセンスの下に公開する。